Jak rozwiązać Wieże Hanoi

Klasyczne Wieże Hanoi - początkowo wszystkie krążki są na słupku 'A'.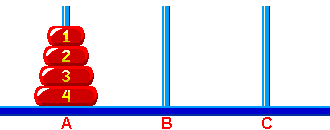

Rys. 1

Rozwiązaniem zagadki jest ustawienie wieży na słupku 'C' w jak najmniejszej liczbie ruchów, gdzie ruchem jest przeniesienie pojedynczego krążka ze słupka na słupek, z ograniczeniem że nie można kłaść większego krążka na mniejszy.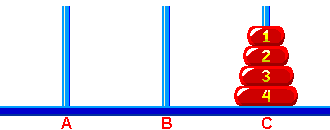

Rys. 2

Dowolne Wieże Hanoi - na początku, krążki mogą być w dowolnej pozycji pod warunkiem, że nigdy większy krążek nie leży na mniejszym (patrz Rys. 3). Na końcu, krążki mogą być w innym dowolnym położeniu - pod tym samym warunkiem.  ^* )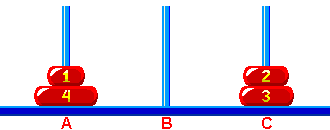

Rys. 3

Rozwiązanie Wieży Hanoi

Rozwiązanie Wież Hanoi - 'regular' na 'perfect'

Zacznijmy myśleć jak rozwiązać tę łamigłówkę.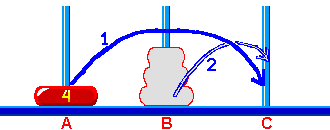
Przyjmijmy, dla uproszczenia, że naszym celem jest ustawienie 4-ro krążkowej wieży na słupku 'C' - tak jak w klasycznej Wieży Hanoi (patrz Rys. 2).
Załóżmy, że 'wiemy' jak przenieść 'doskonałą' 3 krążkową wieżę.
Wtedy na ścieżce rozwiązania jest jeden specjalny układ krążków. Krążek nr 4 jest na słupku 'A' i 3 krążkowa wieża jest na słupku 'B', a docelowy słupek 'C' jest pusty.

Rys. 4

Z tego ustawienia musimy tylko przenieść krążek 4 z 'A' na 'C' i następnie jakąś magiczną sztuczką przenieść 3 krążkową wieżę z 'B' na 'C'.

Cofnijmy się myślą. Zapomnijmy o krążkach większych niż 3.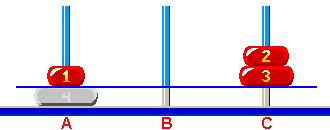
Krążek 3 jest teraz na słupku 'C'. Potrzebujemy by krążek 3 znalazł się na słupku 'B'. Aby to osiągnąć, potrzebujemy by krążek 3 był na miejscu gdzie jest, słupek 'B' powinien być wolny, a krążki 2 i 1 powinny być na słupku 'A'. Tak więc naszym celem jest przeniesienie krążka 2 na słupek 'A'.

Rys. 5

Zapomnijmy na moment o krążku 3 (patrz Rys. 6). Aby móc przenieść krążek 2 na słupek 'A' potrzebujemy zwolnić słupek 'A' (ponad cienką niebieską linią), krążki mniejsze niż krążek 2 ustawione na słupku 'B'. Tak więc, naszym celem jest teraz przeniesienie krążka 1 na słupek 'B'.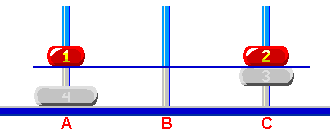
Jak widzimy, jest to proste zadanie gdyż krążek 1 nie ma nad sobą innego i słupek 'B' jest wolny.

Rys. 6

Więc przenieśmy go.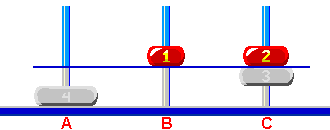

Rys. 7

Opisane powyżej kroki są wykonane przez iteracyjny algorytm zastosowany w Wieże Hanoi, gdy kliknie się guzik "Help me". Ten guzik i funkcja dokonuje analizy aktualnego układu krążków i generuje tylko pojedynczy ruch, który prowadzi najkrótszą drogą do rozwiązania. To jest celowo tak zrobione.

Gdy guzik 'Help me' jest ponownie kliknięty, algorytm powtarza wszystkie kroki analizy rozpoczynając od największego krążka - w tym przykładzie krążek 4 - i generuje następny ruch - krążek 2 ze słupka 'C' na słupek 'A'.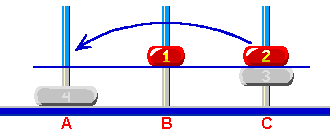

Rys. 8

Jeśli jest potrzebny rekurencyjny lub iteracyjny algorytm , który generuje serię ruchów prowadzących do rozwiązania dowolnego układu Wież Hanoi należy użyć jakiś rodzaj back track programming, tzn. algorytm powinien pamiętać już wykonane kroki analizy i nie powtarzać analizy układu krążków od początku.

Ale to już jest temat na osobne długie opowiadanie.

^*)   Proszę wziąć pod uwagę, że układ krążków może nie być na najkrótszej drodze pomiędzy początkową i końcową pozycją klasycznych Wież Hanoi. Układ taki może się zdarzyć gdy wykona się kilka złych ruchów podczas rozwiązywania klasycznych Wież.

^**)   Legenda, napisana przez Eduarda Lucas - francuskiego matematyka
"W Indiach, w mieście Banares, pod kopułą głównej świątyni, w miejscu, gdzie znajduje się środek Ziemi, postawił Brahma na brązowej tabliczce trzy diamentowe pałeczki o wysokości jednego łokcia i o grubości tułowia pszczoły. Przy stworzeniu świata na jedną z tych pałeczek nanizane zostały 64 krążki z czystego złota z otworami pośrodku tak, iż utworzyły postać ściętego stożka. Kapłani luzując się wzajemnie dniem i nocą bez przystanku, zajęci są przeniesieniem tego stożka z pierwszej pałeczki na trzecią, posiłkując się przejściowo pałeczką drugą, przy czym zobowiązani są najsurowiej przestrzegać dwu następujących zakazów: po pierwsze, za jednym ujęciem nie przenosić nigdy więcej ponad jeden krążek; po wtóre, nigdy nie kłaść krążka większego na mniejszym. Gdy kapłani, zachowując ściśle te przepisy, ukończą swą pracę, nastąpi koniec świata..."

Szczepan Jeleński - Lilavati, Rozrywki Matematyczne